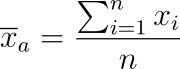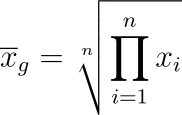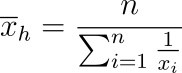We encourage you to engage further in the fundamentals of data science through our channel here. In data science, understanding and summarizing data is a foundational step. Because they help identify a representative value within a dataset, measures of central tendency are crucial in this respect and form a central element of descriptive statistics. Descriptive statistics provide a way to describe and summarize the main features of a dataset, offering a clear picture of its overall structure.

Measures of central tendency are essential for summarizing data, but they are only part of the story. To fully characterize and understand the data, it is equally important to consider measures of variability, which describe the spread or dispersion within the dataset. In this post, we will briefly describe the main measures of central tendency, explaining their definitions, use cases, and advantages. In a subsequent post, we will explore measures of variability, completing our overview of key descriptive statistics.

By comprehending both central tendency and variability, one can gain a more comprehensive understanding of the dataset, making it easier to draw meaningful insights and make informed decisions.

Die Bedeutung der Wahl der richtigen Metrik

Verschiedene Metriken der zentralen Tendenz sind für verschiedene Arten von Daten geeignet. Die Wahl der Metrik hängt von Faktoren wie der Verteilung der Daten, dem Vorhandensein von Ausreißern und den inhärenten Merkmalen der Daten selbst ab. Jede Metrik kann unterschiedlich funktionieren, je nachdem, ob die Daten schief sind, Ausreißer aufweisen, einem bestimmten Verteilungsmuster folgen oder einzigartige Merkmale aufweisen. Die Wahl einer geeigneten Messgröße kann eine klarere und genauere Darstellung der Daten liefern und sicherstellen, dass die gewonnenen Erkenntnisse aussagekräftig und zuverlässig sind. Wenn Sie sich jedoch nur auf die Metrik der zentralen Tendenz verlassen, erhalten Sie oft kein vollständiges Bild des Datensatzes. Um die Daten vollständig zu verstehen, ist es unerlässlich, diese Maße durch Maße der Variabilität zu ergänzen. Variabilitätsmaße ermöglichen es uns zu verstehen, wie die Datenpunkte um die zentrale Tendenz herum gestreut sind, was unserer Analyse zusätzlichen Kontext und Tiefe verleiht. In diesem Beitrag werden wir die wichtigsten Maße der zentralen Tendenz erörtern und ihre Eigenschaften untersuchen. Wenn wir diese Messgrößen und ihre Rolle bei der Zusammenfassung von Daten verstehen, können wir ihre Stärken und Grenzen in verschiedenen Datenszenarien besser einschätzen.

Die Wichtigste Maße der zentralen Tendenz

Zu den wichtigsten Maßen der zentralen Tendenz gehören der Modus, der Median, das arithmetische Mittel, das geometrische Mittel und das harmonische Mittel. Jedes dieser Maße hat seine eigenen Eigenschaften und eignet sich für verschiedene Arten von Daten. Im Folgenden werden wir jedes dieser Maße im Detail untersuchen und ihre Definitionen, Anwendungsfälle, Vor- und Nachteile erörtern.

Arithmetisches Mittel

• Definition: Das arithmetische Mittel ist die Summe aller Werte geteilt durch die Anzahl der Werte.
• Anwendungsfälle: Es funktioniert gut bei symmetrischen Verteilungen ohne extreme Ausreißer.
• Vor- und Nachteile: Das arithmetische Mittel ist einfach zu berechnen und zu verstehen. Es kann jedoch durch Ausreißer und schiefe Daten stark beeinflusst werden.

Geometrischer Mittelwert

• Definition: Das geometrische Mittel ist die n-te Wurzel aus dem Produkt von n Werten.
• Anwendungsfälle: Es eignet sich für Daten, die multiplikativ sind oder eine Log-Normal-Verteilung haben.
• Vor- und Nachteile: Das geometrische Mittel kann mit schiefen Daten besser umgehen als das arithmetische Mittel, aber es kann keine negativen oder Nullwerte verarbeiten.

Harmonischer Mittelwert

• Definition: Das harmonische Mittel ist der Kehrwert des arithmetischen Mittels der Kehrwerte der Datenwerte.
• Anwendungsfälle: Es eignet sich am besten für Raten und Verhältnisse, wie Geschwindigkeiten oder Dichten.
• Vor- und Nachteile: Das harmonische Mittel reagiert empfindlich auf niedrige Werte und kann keine Nullen verarbeiten. Es ist in bestimmten Szenarien wie z.B. Durchschnittswerten nützlich.

Median

• Definition: Der Median ist der mittlere Wert, wenn die Daten vom kleinsten zum größten Wert geordnet sind.
• Anwendungsfälle: Es ist ideal für schiefe Verteilungen, da es nicht von Ausreißern beeinflusst wird.
• Vor- und Nachteile: Der Median ist robust gegenüber Ausreißern und schiefen Daten, aber er kann bei kleinen Datensätzen weniger informativ sein.

Modus

• Definition: Der Modus ist der am häufigsten vorkommende Wert in einem Datensatz.
• Anwendungsfälle: Es ist besonders nützlich für kategorische Daten oder Datensätze mit einer hohen Häufigkeit bestimmter Werte.
• Vor- und Nachteile: Der Modus ist einfach zu verstehen und zu berechnen. Bei kontinuierlichen Daten mit vielen eindeutigen Werten liefert er jedoch möglicherweise kein klares Bild.

Praktische Beispiele: Die Wahl des richtigen Maßes für die zentrale Tendenz

Beispiel 1. Normalverteilung

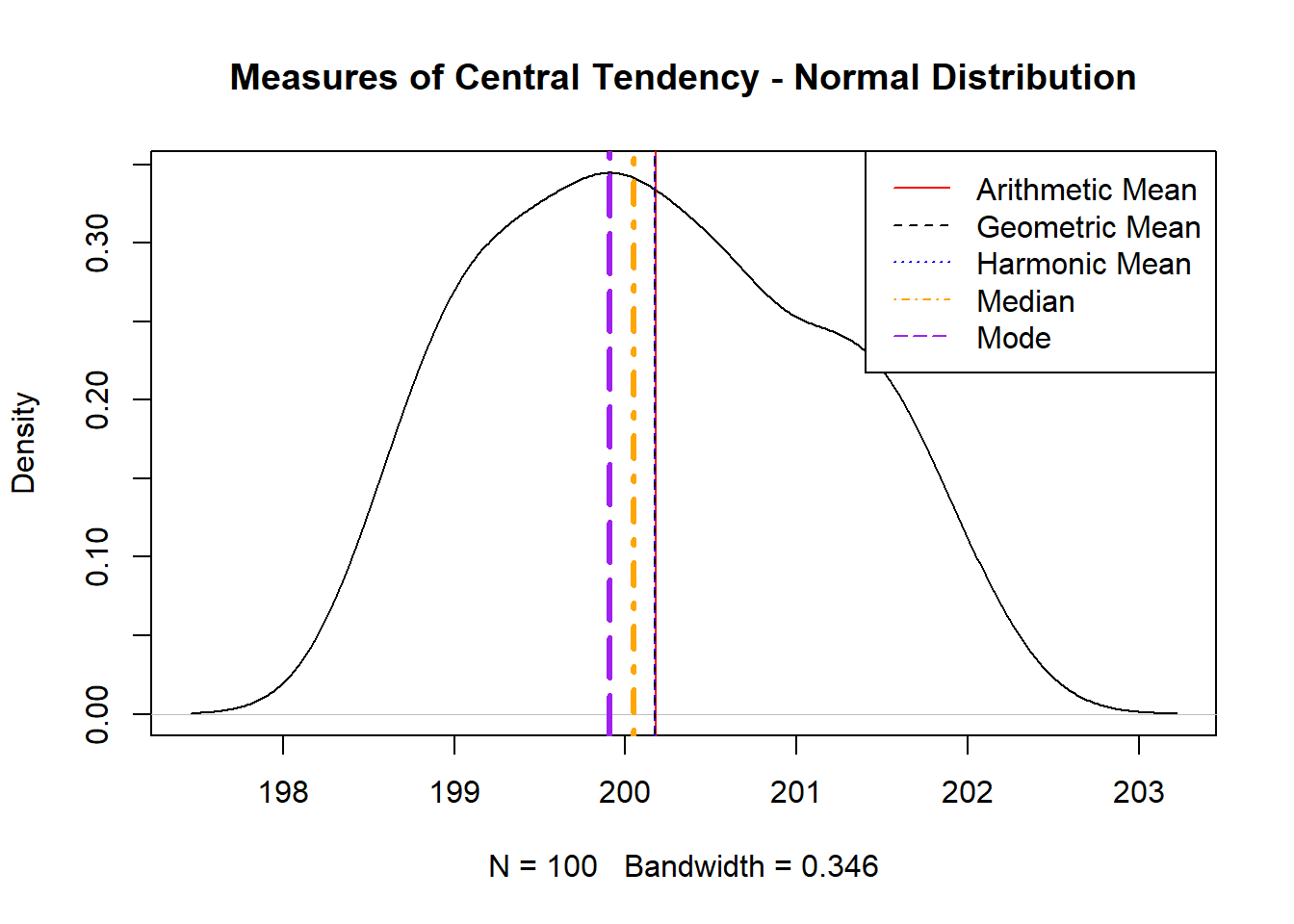
Stellen Sie sich einen Datensatz vor, der einer annähernden Normalverteilung folgt, die oft als glockenförmige Dichtekurve dargestellt wird. In diesem Szenario könnten mehrere Maße für die zentrale Tendenz geeignet sein, aber die Wahl des am besten geeigneten hängt vom Verständnis der Merkmale der Verteilung ab:

1. Arithmetisches Mittel: Bei einer vollkommenen Normalverteilung ist das arithmetische Mittel oft das bevorzugte Maß. Dies liegt daran, dass es alle Datenpunkte berücksichtigt und einen ausgewogenen zentralen Wert liefert. Bei einer symmetrischen Verteilung repräsentiert der Mittelwert genau die Mitte des Datensatzes.
2. Median: Während der Median weniger empfindlich auf Ausreißer reagiert, sind Ausreißer in einer normalen Verteilung in der Regel weniger verbreitet. Wenn es jedoch leichte Abweichungen von der Normalität gibt, kann der Median immer noch einen robusten zentralen Wert liefern, der von kleinen Schräglagen oder Ausreißern unbeeinflusst bleibt.
3. Modus: Bei einer unimodalen Normalverteilung fällt der Modus (der häufigste Wert) mit dem Mittelwert und dem Median zusammen. Der Modus ist zwar nützlich, um die Spitze der Verteilung zu identifizieren, bietet aber im Vergleich zu Mittelwert und Median in diesem Zusammenhang weniger umfassende Informationen.
4. Geometrische und harmonische Mittelwerte: Diese Maße werden in der Regel nicht für normalverteilte Daten verwendet, da sie eher für multiplikative Daten, lognormale Verteilungen oder Datensätze mit Raten oder Verhältnissen geeignet sind. Beachten Sie, dass bei einer Normalverteilung mit geringer Varianz und eng geclusterten Werten das arithmetische Mittel, das geometrische Mittel und das harmonische Mittel ähnliche Werte liefern können. Wenn jedoch die Varianz zunimmt oder die Verteilung schief wird, werden die Unterschiede zwischen diesen Mittelwerten deutlicher. Das arithmetische Mittel bleibt im Allgemeinen das beste Maß für die zentrale Tendenz bei normal verteilten Daten.

In diesem Fall ist für einen Datensatz, der einer zufälligen Normalverteilung folgt, das arithmetische Mittel im Allgemeinen die beste Wahl. Es nutzt alle Datenpunkte und bietet einen präzisen zentralen Wert, der gut mit der symmetrischen Natur der Verteilung übereinstimmt. Bestehen jedoch Bedenken wegen Ausreißern oder einer leichten Schräglage, ist der Median eine gute Alternative.

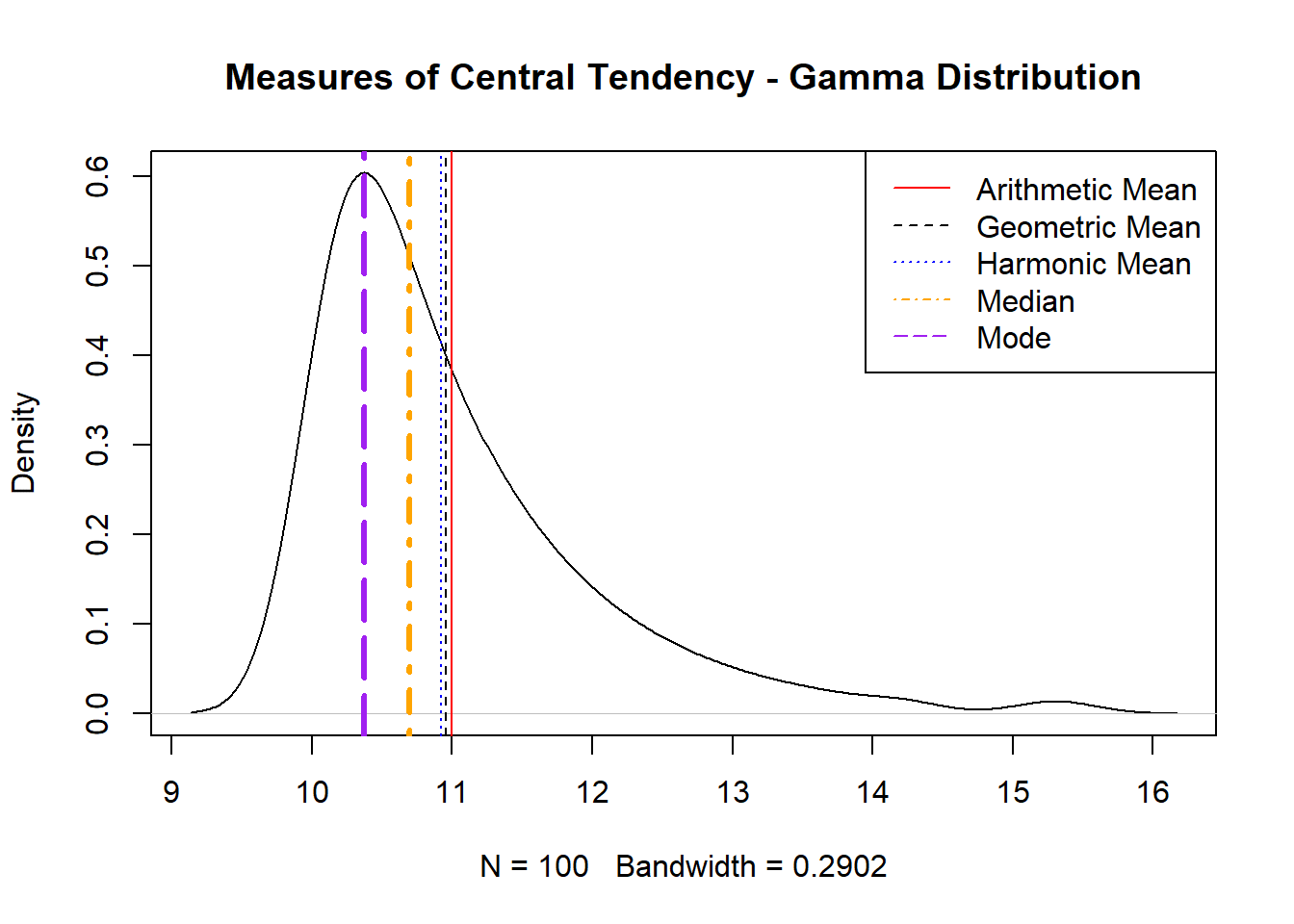
Beispiel 2. Gamma-Verteilung

Nehmen Sie einen Datensatz an, der einer Gamma-Verteilung folgt, die häufig zur Modellierung schiefer Daten wie Wartezeiten oder Lebensdauern verwendet wird. Die Gamma-Verteilung wird durch ihre Form- und Skalenparameter charakterisiert, die ihre Schiefe beeinflussen. Die Wahl des geeigneten Maßes für die zentrale Tendenz einer solchen Verteilung erfordert das Verständnis ihrer einzigartigen Eigenschaften:

1. Arithmetisches Mittel: Das arithmetische Mittel wird in der Regel für Gamma-Verteilungen verwendet, kann aber durch die Schiefe der Daten beeinträchtigt werden. Es liefert zwar einen Durchschnittswert, aber bei stark schiefen Verteilungen repräsentiert es den typischen Datenpunkt möglicherweise nicht genau.
2. Median: Der Median ist ein robustes Maß für Gamma-Verteilungen, insbesondere wenn die Verteilung stark schief ist. Er liefert einen zentralen Wert, der weniger von Extremwerten beeinflusst wird und eine repräsentativere zentrale Tendenz für schiefe Daten bietet.
3. Modus: Bei unimodalen Gamma-Verteilungen identifiziert der Modus (der häufigste Wert) effektiv die Spitze der Verteilung. Bei stark schiefen Verteilungen kann der Modus den wahrscheinlichsten Wert hervorheben, der oft informativer ist als der Mittelwert.
4. Geometrischer Mittelwert: Das geometrische Mittel kann für Gamma-Verteilungen relevant sein, wenn es um multiplikative Prozesse geht. Es betont die zentrale Masse der Daten, aber wie das arithmetische Mittel liefert es bei schiefen Verteilungen nicht immer einen intuitiven zentralen Wert.
5. Harmonischer Mittelwert: Der harmonische Mittelwert wird im Allgemeinen nicht für Gamma-Verteilungen verwendet. Es eignet sich eher für Datensätze, die Raten oder Verhältnisse beinhalten und bietet möglicherweise kein aussagekräftiges Maß für die zentrale Tendenz bei dieser Art von Daten.

Bei einer Gamma-Verteilung hängt die Wahl zwischen Mittelwert, Median und Modus stark vom Grad der Schiefe ab. Bei mäßig schiefen Verteilungen kann das arithmetische Mittel gute Dienste leisten, während bei stark schiefen Verteilungen der Median eine genauere zentrale Tendenz liefert. Der Modus ist besonders nützlich, um den wahrscheinlichsten Wert in schiefen Verteilungen zu ermitteln.

Other Metrics

Apart from the main measures of central tendency, there are other metrics that can be useful in specific situations. These metrics include the trimmed mean, winsorized mean, and weighted mean. While they may not be as commonly used as the primary measures, they offer additional tools for dealing with outliers and weighted data.

• Trimmed Mean: This is the mean calculated after removing a specified percentage of the smallest and largest values, which helps in reducing the effect of outliers.
• Winsorized Mean: Similar to the trimmed mean, but instead of removing outliers, extreme values are replaced with the nearest remaining values.
• Weighted Mean: This mean gives more importance to some values over others, making it useful when certain values in the dataset are more significant.

Conclusion

In summary, choosing the appropriate measure of central tendency is essential for accurate data analysis. Adhering to recognized standards and practices within the scientific community ensures that the selected metric aligns well with the specific characteristics of the dataset, whether it exhibits skewness, contains outliers, or conforms to a particular distribution.

Nevertheless, relying solely on measures of central tendency may not offer a comprehensive view of the data. Supplementary measures such as measures of variability are indispensable for capturing the complete spectrum and dispersion of data points, thereby enriching the overall understanding of the dataset.

When confronted with datasets that are challenging to characterize, advanced techniques beyond descriptive statistics can be employed. These methods not only modify and refine the original data but also enhance its suitability for analysis, prediction, and the development of robust algorithms.